Kointegrierte Prozesse
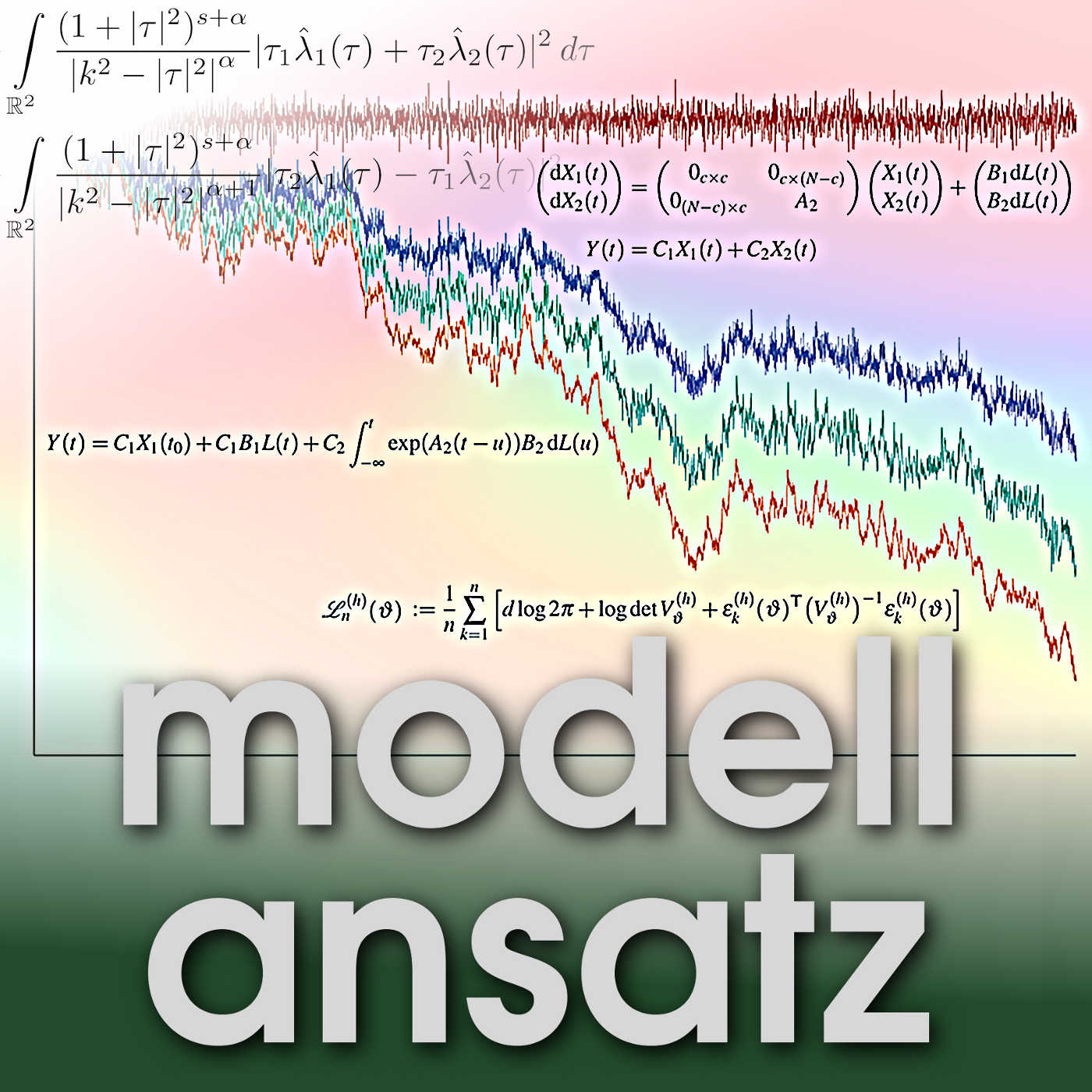
Markus Scholz hat gerade seine Dissertation Estimation of Cointegrated Multivariate Continuous-Time Autoregressive Moving Average Processes an der KIT-Fakult\xe4t f\xfcr Mathematik verteidigt. Gudrun ergriff die Gelegenheit, mit ihm \xfcber die Idee und Anwendungsm\xf6glichkeiten von Zeitreihen-Modellen zu sprechen. Prinzipiell stehen Zeitreihen einerseits f\xfcr zeitlich geordnete (Mess-)Daten, die z.B. durch Abtasten (wiederholtes Messen) eines Vorgangs in der Realit\xe4t entstehen. Andererseits werden sie in der Statistik als Ergebnis eines Stochastischen Prozesses interpretiert, der diese Zeitreihe als eine seiner Realisierungen erzeugt. Der stochastische Prozess ist hierbei ein Modell und soll die wichtigsten Eigenschaften der Daten erfassen. Er soll auch dazu dienen, zuverl\xe4ssige Sch\xe4tzungen zu liefern, wie sich die Zeitreihe wahrscheinlich in die Zukunft fortsetzt. Mitunter interessieren hier sogar nur so oberfl\xe4chliche Informationen wie Saisonalit\xe4t und Trends. Ein Aspekt, der im Titel der Arbeit von Markus Scholz als "Moving Average" beschrieben ist, ist die Eigenschaft, dass die Werte der Zeitreihe vor allem durch die letzten davor liegenden Me\xdfpunkte beeinflusst sind und die "Erinnerung" an weiter in der Vergangenheit liegende Zust\xe4nde abklingt. Im Modell ist hier stets eine Zufallsquelle integriert, die man sich wie ein Ausw\xfcrfeln pro Zeitpunkt vorstellen kann. Wie erfolgt hier die Zuordnung zwischen Datenreihe und stochastischem Modell? In der Regel basiert die Wahl auf der Erfahrung \xfcber zuvor benutzte Modelle in \xe4hnlichen Zusammenh\xe4ngen und auf den bekannten Eigenschaften der Modelle. Anschlie\xdfend m\xfcssen jedoch stochastische Tests belegen, dass die Zuordnung tats\xe4chlich korrekt ist. Markus Scholz hat sich mit stochastischen Prozessen besch\xe4ftigt, die kontinuierlich in der Zeit sind statt - wie bisher beschrieben - diskret. Sie eignen sich z.B. zur Modellierung von Temperaturverl\xe4ufen. Prinzipiell nimmt man dabei an, dass eine hoch genug gew\xe4hlte Abtastrate den \xdcbergang von diskreten Messungen zu einem als stetig angesehenen Prozess unkritisch macht. Der Aspekt, der ihn hier vor allem besch\xe4ftigt hat, war die Erweiterung bekannter Modelle um die Eigenschaft der Nicht-Stationarit\xe4t. Das hei\xdft kurz gesagt, die Grundeigenschaften des Prozesses k\xf6nnen sich \xfcber die Zeit \xe4ndern. Das kennen wir ja auch von der Temperatur: Einerseitzs durchlaufen t\xe4gliche Tiefst-, H\xf6chst- oder Mittelwerte der Temperatur im Jahresverlauf eine typische Kurve f\xfcr eine betrachtete Region. Andererseits kann im konkreten Jahr ein untypischer Verlauf vorliegen und es ist gar nicht so leicht zu quantifizieren, ob es sich um eine untypische Beobachtung handelt oder sich z.B. die Mittelwerte tats\xe4chlich statistisch signifikant \xe4ndern. Anders gesagt f\xfchrt die Nicht-Stationarit\xe4t im Modell auf Probleme bei zugeh\xf6rigen Sch\xe4tzungen, die in der Regel schwer zu l\xf6sen sind. Deshalb hat Markus Scholz zun\xe4chst einen handhabbaren Spezialfall ausgew\xe4hlt, sogenannten kointegrierte Prozesse...